Biografía de GAUSS

“ JOHANN  CARL  FRIEDRICH  GAUSS ”

(1777-1855)

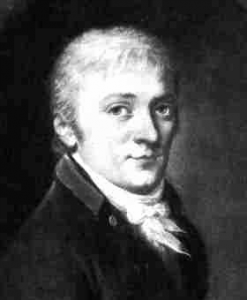
El más grande matemático del siglo XIX, Johann Carl Friedrich Gauss se considera uno de los tres matemáticos más importante de todos los tiempos, siendo Arquímedes y Newton los otros dos.

Gauss nació en Brunswick, Alemania, en 1777. Su padre, un obrero amante del trabajo, era excepcionalmente obstinado y no creía en la educación formal, hizo todo lo que pudo para evitar que Gauss fuera a una buena escuela. Por fortuna para Carl (y para las matemáticas), su madre a pesar de que tampoco contaba con educación, apoyó a su hijo en sus estudios y se mostró siempre orgullosa de sus logros hasta el día de su muerte a los 97 años.

Gauss era un niño prodigio. A los 3 años encontró un error en la libreta de cuentas de su padre. Una anécdota famosa habla de Carl, de 10 años de edad, como estudiante de la escuela local de Brunswick. El profesor solía asignar tareas par mantener ocupados a los alumnos. Un día les pidió que sumaran los números del 1 al 100. Casi al instante, Carl colocó su pizarra cara abajo con las palabras “ya está”. Después, el profesor descubrió que Gauss era el único con la respuesta correcta, 5 050. Gauss había observado que los números se podían arreglar en 50 pares que sumaban cada uno 101 (1+100, 2+99, etc.), y 50 x 101 = 5 050. Años después, Gauss bromeaba diciendo que podía sumar más rápido de lo que podía hablar.

Cuando Gauss tenía 15 años, el Duque de Brunswick se fijó en él y lo convirtió en su protegido. El Duque lo ayudó a ingresar  en el Brunswick College en 1795 y, tres años después, a entrar a la universidad de Gottingen. Indeciso entre las carreras de matemáticas y filosofía, Gauss eligió la de matemáticas después de dos descubrimientos asombrosos. Primero inventó el método de mínimos cuadrados una década antes de que  Legendre publicara sus resultados. Segundo, un mes antes de cumplir 19 años, resolvió un problema cuya solución se había buscado durante más de dos mil años: Gauss demostró cómo construir, con sólo regla  y compás, un polígono regular cuyo número de lados no es múltiplo de 2, 3 o 5. El 30 de marzo de 1796, el día de este descubrimiento, comenzó un diario que contenía como primera nota las reglas de construcción de un polígono regular de 17 lados. El diario, que contiene los enunciados de 146 resultados en solo 19 páginas, es uno de los documentos más importantes en la historia de las matemáticas.

Después de un corto periodo en Gottingen, Gauss fue a la University of Helmstadt y, en 1798, a los 20 años, escribió su famosa disertación doctoral. En ella dio la primera demostración matemática rigurosa del teorema fundamental del álgebra -que todo polinomio de grado n tiene, contando multiplicidad, exactamente n raíces. Muchos matemáticos incluyendo a Euler, Newton y Lagrange, habían intentado probar ese resultado.

Gauss hizo un gran número de descubrimientos en física al igual que en matemáticas. Por ejemplo, en 1801 utilizó un nuevo procedimiento para calcular, a partir de unos cuantos datos, la órbita del planetoide Ceres. En 1833 inventó el telégrafo electromagnético junto con su colega Wilhelm Weber (1804-1891). Aunque realizó trabajos brillantes en astronomía y electricidad, fue la producción matemática de Gauss la que resultó asombrosa.

Hizo contribuciones fundamentales al álgebra y la geometría. En 1811 descubrió un resultado que llevó a Cauchy a desarrollar la teoría de variable compleja. En álgebra lineal podemos encontrar el método de eliminación de Gauss-Jordan. Los estudiantes de análisis numérico aprenden la cuadratura gaussiana – una técnica de integración numérica.

Gauss fue nombrado catedrático de matemáticas en Gottingen en 1807 e impartió clases hasta su muerte en 1855. Aún después de fallecer, su espíritu matemático siguió acosando a los matemáticos del siglo XIX. Con frecuencia, un importante resultado nuevo ya había sido descubierto por Gauss y se podía encontrar en sus notas inéditas.

En sus escritos matemáticos Gauss era un perfeccionista y tal vez sea el último matemático que sabía todo sobre su área. Afirmando que una catedral no lo era hasta que se quitaba el último de los andamios, ponía todo su empeño para que cada uno de sus trabajos publicados fuera completo, conciso y elegante. Usaba un sello en el que se veía un árbol con unas cuantas frutas y la leyenda paula sed matara (pocas pero maduras). Gauss creía también que las matemáticas deben reflejar el mundo real. A su muerte, Gauss fue honrado con una medalla conmemorativa con la inscripción “George V, Rey de Hanover, al príncipe de los matemáticos”.